Algorithm/Baekjoon
[백준 3653 : JAVA] 영화 수집 / 세그먼트 트리
팡트루야
2021. 3. 30. 21:42
문제
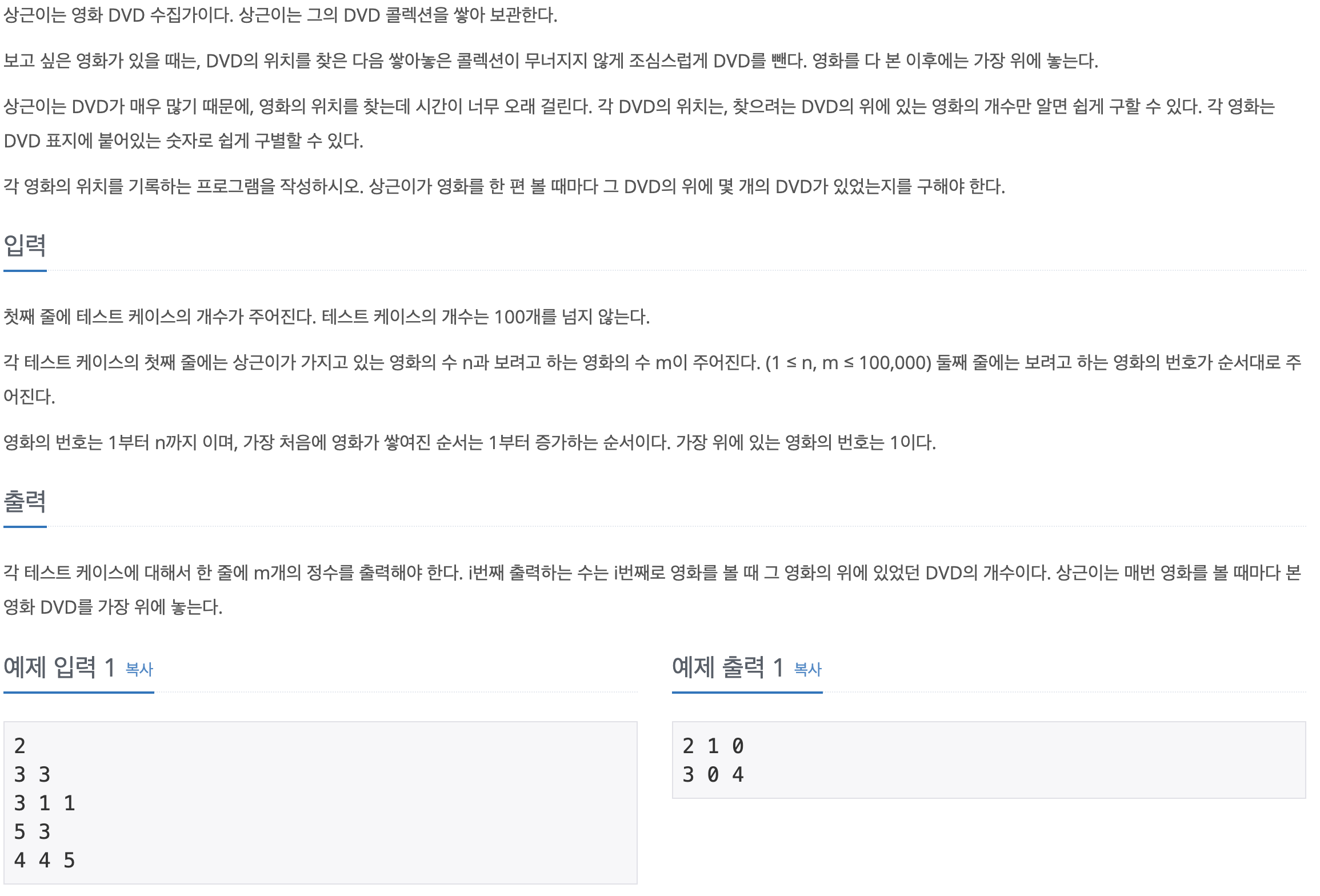
풀이
세그먼트 트리 응용문제로, 창의성을 요구하는 문제다.

한 번 보고난 영화 DVD는 위로 옮겨져야 하기 때문에 옮겨질(m)만큼의 크기도 추가해 배열을 할당한다.
3번 영화를 보고난 후에는 3번 영화의 인덱스를 변경해줘야 하기 때문에, 각 [영화 번호, 인덱스] 쌍을 알고 있어야 한다.
영화번호-인덱스 쌍을 저장하기 위해 Map(=Dictionary) 자료구조를 이용하는 대신, 좀 더 원시적인 방법인 배열을 이용했다.
for (int i = 1; i <= n; i++) {
moviePosInStack[i] = m + i - 1; // 배열[영화번호] = 인덱스
}
코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
private static int n, m;
private static SegmentTree tree;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine());
while (T-- > 0) {
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
int[] movieStack = new int[n + m];
int[] moviePosInStack = new int[n + 1];
for (int i = 1; i <= n; i++) {
movieStack[m + i - 1] = 1;
moviePosInStack[i] = m + i - 1; // [영화번호, 인덱스] 쌍을 담는다.
}
tree = new SegmentTree(movieStack, n + m);
tree.init(1, 0, n + m - 1);
st = new StringTokenizer(br.readLine());
for (int i = 0; i < m; i++) {
int selectedMovie = Integer.parseInt(st.nextToken());
// Query
int result = tree.query(0, moviePosInStack[selectedMovie] - 1, 1, 0, n + m - 1);
// Update
tree.update(moviePosInStack[selectedMovie], 0, 1, 0, n + m - 1);
moviePosInStack[selectedMovie] = (m - 1) - i; // 해당 DVD의 위치(인덱스)를 가장 위로 옮긴다.
tree.update(moviePosInStack[selectedMovie], 1, 1, 0, n + m - 1);
sb.append(result).append(" ");
}
sb.append("\n");
}
System.out.println(sb.toString());
}
private static class SegmentTree {
int[] arr;
int[] tree;
public SegmentTree(int[] arr, int n) {
this.arr = arr;
int k = (int) Math.ceil(Math.log(n) / Math.log(2));
int height = k + 1;
int size = (int) Math.pow(2, height);
tree = new int[size];
}
public int init(int node, int start, int end) {
if (start == end) {
return tree[node] = arr[start];
}
int mid = (start + end) / 2;
return tree[node] = init(node * 2, start, mid) + init(node * 2 + 1, mid + 1, end);
}
public int update(int idx, int newValue, int node, int start, int end) {
if (idx < start || end < idx) return tree[node];
if (start == end) return tree[node] = newValue;
int mid = (start + end) / 2;
return tree[node] = update(idx, newValue, node * 2, start, mid) + update(idx, newValue, node * 2 + 1, mid + 1, end);
}
public int query(int left, int right, int node, int start, int end) {
if (right < start || end < left) return 0;
if (left <= start && end <= right) return tree[node];
int mid = (start + end) / 2;
return tree[node] = query(left, right, node * 2, start, mid) + query(left, right, node * 2 + 1, mid + 1, end);
}
}
}