[백준 2661 : C++] 좋은수열 / 백트래킹
문제

풀이
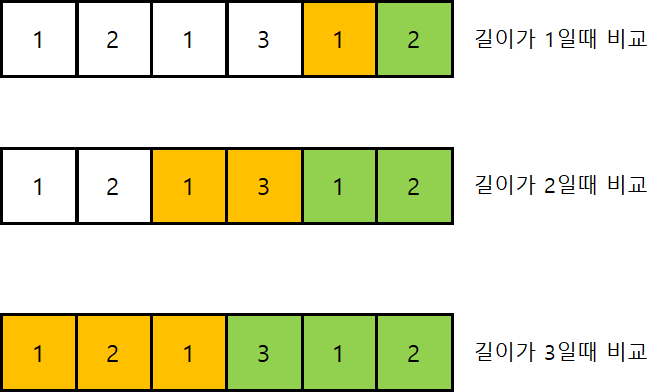
이 문제의 핵심은 좋은수열인지 판별하는 방법을 알아내는 것이다.
마지막 인덱스를 기준으로 길이를 1부터 시작해 (수열의 길이 / 2)까지 비교한다.
코드
C++ 언어를 이용하여 코드를 살펴보자.
#include <iostream>
#include <string>
using namespace std;
int N;
string s;
bool flag;
void func(string t, int depth) {
if (flag) return;
int len = t.size();
for (int i = 1; i <= (len / 2); i++) {
if (t.substr(len - i, i) == t.substr(len - (2 * i), i)) {
t = "";
return;
}
}
if (depth > N) return;
if (depth == N) {
flag = true;
cout << t << "\n";
return;
}
else {
for (int i = 0; i < N; i++) {
func(t + "1", depth + 1);
func(t + "2", depth + 1);
func(t + "3", depth + 1);
}
}
}
int main() {
cin >> N;
func(s, 0);
return 0;
}'Algorithm > Baekjoon' 카테고리의 다른 글
| [백준 2206 : JAVA] 벽 부수고 이동하기 / BFS (0) | 2020.09.08 |
|---|---|
| [백준 9370 : JAVA] 미확인 도착지 / 다익스트라 (0) | 2020.08.28 |
| [백준 11057 : C++] 오르막 수 / DP (0) | 2019.10.24 |
| [백준 11559 : C++] Puyo Puyo / BFS, DFS (0) | 2019.10.18 |
| [백준 2749 : C++] 피보나치 수 3 (0) | 2019.08.29 |
댓글
이 글 공유하기
다른 글
-
[백준 9370 : JAVA] 미확인 도착지 / 다익스트라
[백준 9370 : JAVA] 미확인 도착지 / 다익스트라
2020.08.28 -
[백준 11057 : C++] 오르막 수 / DP
[백준 11057 : C++] 오르막 수 / DP
2019.10.24 -
[백준 11559 : C++] Puyo Puyo / BFS, DFS
[백준 11559 : C++] Puyo Puyo / BFS, DFS
2019.10.18 -
[백준 2749 : C++] 피보나치 수 3
[백준 2749 : C++] 피보나치 수 3
2019.08.29