[백준 12865 : JAVA] 평범한 배낭
1. 문제
이 문제는 아주 평범한 배낭에 관한 문제이다.
한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다. 준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K만큼의 무게만을 넣을 수 있는 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.
2. 입력
첫 줄에 물품의 수 N($1 \le N \le 100$)과 준서가 버틸 수 있는 무게 K($1 \le K \le 100000$)가 주어진다.
두 번째 줄부터 N개의 줄에 걸쳐 각 물건의 무게 W($1 \le W \le 100000$)와 해당 물건의 가치 V($0 \le V \le 1000$)가 주어진다.
입력으로 주어지는 모든 수는 정수이다.
3. 출력
한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.
4. 풀이
배낭 문제는 아주 유명한 DP 입문용 문제입니다. (쉽다는 뜻은 아닙니다.. 😅 )
DP로 문제를 풀기 위해서는 최적의 원리(Principle of Optimality)를 만족해야 합니다.
최적의 원리(Principle of Optimality)란 다음과 같습니다.
"어떤 문제의 입력 사례의 최적해가 그 입력 사례를 분할한 부분 사례에 대한 최적해를 항상 포함하고 있다"
집합 A를 n개의 보석들 중에서 고른 최적의 부분 집합이라고 가정해보겠습니다.
- 집합 A가 n번째 보석을 포함하고 있지 않다면, A는 n-1개의 보석들 중에서 최적으로 고른 부분 집합과 같다.
즉, n-1번째까지의 최적해다. - 집합 A가 n번째 보석을 포함하고 있다면, n-1개의 보석들 중에서 최적으로 고른 가격의 합에다가 n번째 보석 가격을 더한 것과 같다.
이때, 배낭은 n번째 보석이 들어갈만큼의 여유를 가지고 있어야한다.
위 문장을 식으로 풀어보면 다음과 같습니다.
$$P[i, w]=\begin{cases}P[i-1, w] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ w_{i} \gt w \\max\{v_{i}+P[i-1, w-w_{k}], P[i-1, w]\} \ \ \ else\end{cases}$$
P[i, w]란 i개의 보석이 있고 배낭의 무게 한도가 w일 때 최적의 이익을 의미합니다.
총 4개의 보석이 있고 배낭의 무게 한도가 5kg일때를 예시로 살펴보겠습니다. (각 보석의 무게와 가치는 표 옆에 표시해두었습니다.

우선, 0번째 보석은 없고, 배낭의 무게한도가 0일때 아무런 보석도 담을 수 없으므로 1행과 1열은 모두 0입니다.
1번째 보석일때, 배낭의 무게한도가 1이라면 이 또한 보석을 담을 수 없기 때문에 0입니다. (1번째 보석의 무게는 2kg)

배낭의 무게한도가 2kg라면 1번째 보석을 담을 수 있으니 1번째 보석의 가치만큼이 더해집니다.
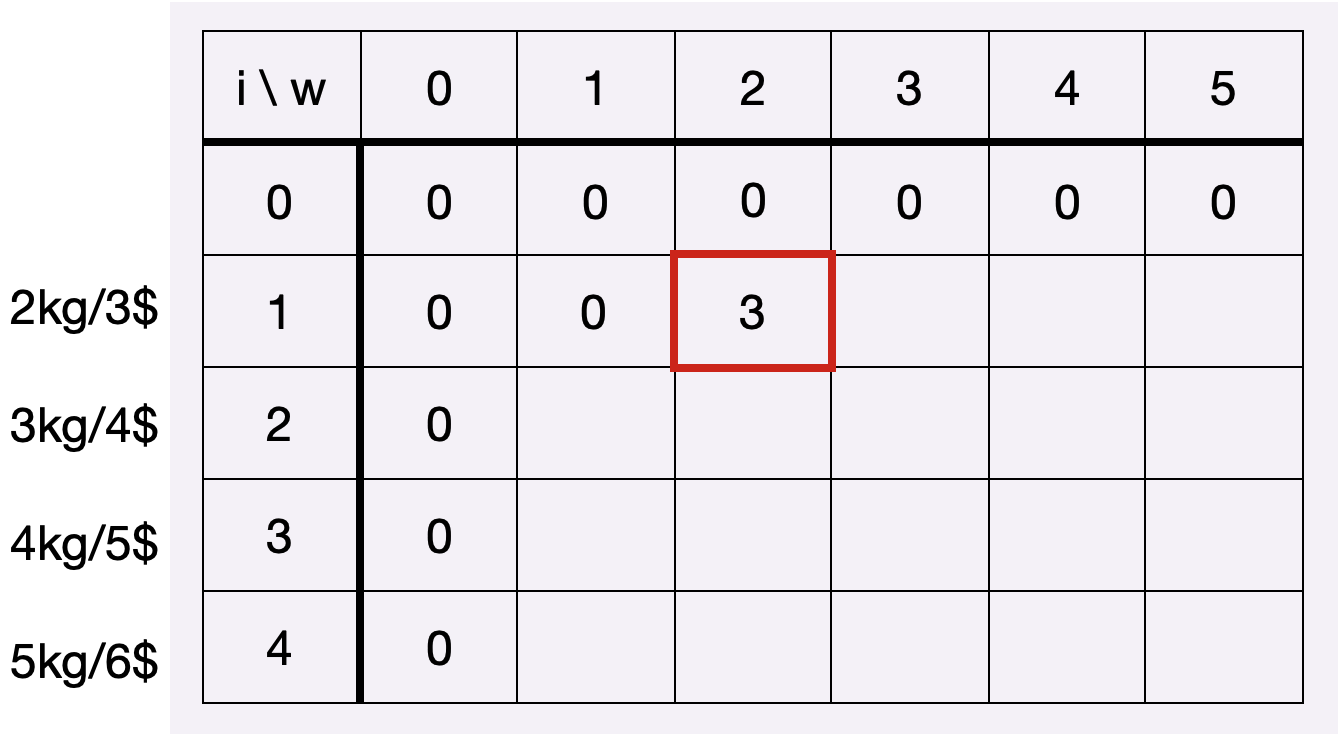
나머지는 똑같은 원리로 채우면 되니 넘어가고, 2번째 보석일때 배낭의 무게한도가 2kg일때를 보겠습니다.

위 빈칸의 값은 무엇일까요? 🤔
배낭의 무게한도가 2kg라면 2번째 보석을 담을 수 없습니다. 따라서, 위에서 살펴본 최적의 원리로 인해 n-1번째의 최적해와 같게 됩니다.
즉, 1번째 보석일때의 똑같이 배낭의 무게한도가 2kg일때의 최적해를 가지고옵니다. 표에서는 해당 칸 바로 윗칸의 값을 가져옵니다.

다음으로 2번째 보석일때, 배낭의 무게한도가 3kg인 경우를 살펴보겠습니다.

배낭의 무게한도가 3kg라면 2번째 보석을 담을 수 있습니다.
이때 다음의 두 값을 비교합니다.
1. 배낭의 무게한도가 0kg일때 i-1번째 보석의 최적해 + i번째 보석의 가치 (i번째 보석의 무게가 3kg라 해당 칸의 무게한도-3kg해서 0kg)
2. 똑같이 배낭의 무게한도가 3kg일때 i-1번째 보석의 최적해
위 로직이 배낭문제의 전부입니다. (나머지 칸들은 위와 같은 방식으로 하시면 채워나가실 수 있으실겁니다. 🙂 )
5. 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
// 배낭 문제
public class Main {
private static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
private static int N, K; // N:보석의 수, K:배낭에 담을 수 있는 무게
private static int[][] dp;
private static Node[] items;
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(in.readLine());
N = Integer.parseInt(st.nextToken());
K = Integer.parseInt(st.nextToken());
dp = new int[N + 1][K + 1];
items = new Node[N + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(in.readLine());
int weight = Integer.parseInt(st.nextToken()); // 무게
int value = Integer.parseInt(st.nextToken()); // 가치
items[i] = new Node(weight, value);
}
for (int i = 1; i <= N; i++) {
int weight = items[i].weight; // i번째 보석의 무게
int value = items[i].value; // i번째 보석의 가치
for (int j = 1; j <= K; j++) {
if (j - weight >= 0) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight] + value);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
System.out.println(dp[N][K]);
}
private static class Node {
int weight, value;
public Node(int weight, int value) {
this.weight = weight;
this.value = value;
}
}
}'Algorithm > Baekjoon' 카테고리의 다른 글
| [백준 15486 : JAVA] 퇴사 2 (0) | 2021.09.06 |
|---|---|
| [백준 17626 : JAVA] Four Squares (0) | 2021.09.06 |
| [백준 12100 : JAVA] 2048 (Easy) (0) | 2021.08.16 |
| [백준 10972 : JAVA] 다음 순열 (0) | 2021.08.09 |
| [백준 1931 : JAVA] 회의실 배정 / 그리디 (0) | 2021.08.03 |
댓글
이 글 공유하기
다른 글
-
[백준 15486 : JAVA] 퇴사 2
[백준 15486 : JAVA] 퇴사 2
2021.09.06 -
[백준 17626 : JAVA] Four Squares
[백준 17626 : JAVA] Four Squares
2021.09.06 -
[백준 12100 : JAVA] 2048 (Easy)
[백준 12100 : JAVA] 2048 (Easy)
2021.08.16 -
[백준 10972 : JAVA] 다음 순열
[백준 10972 : JAVA] 다음 순열
2021.08.09