[알고리즘] 백트래킹(Backtracking)
1. 백트래킹(Backtracking) 알고리즘이란?
DFS(깊이 우선 탐색)를 기반으로 하는 알고리즘으로, DFS의 구조를 적용할 수 있는 문제에 적용될 수 있다.
후보해의 집합에서 최적해 집합을 찾아내는 문제에 사용될 수 있다.
- 후보해 : 해가 될 가능성이 있는 모든 조합
- 최적해 : 문제에서 정하는 답으로서의 기준을 만족하는 해
백트래킹 알고리즘의 핵심은 흔히들 '가지치기'라고들 한다. 그럼 '가지치기'란 뭘까?
가지치기란 말은 백트래킹이 트리 구조를 기반으로 하기 때문에 트리(나무)에서 애초에 조건에 맞지않는 노드는 가지를 쳐버리자(더 이상 DFS로 깊이 탐색을 진행하지 말자)는 뜻이다. 쉽게 말해 DFS + 조건문인 셈이다.
2. 문제 풀이로 이해하는 백트래킹 알고리즘
N-Queen 문제는 백트래킹 알고리즘으로 해결할 수 있는 문제의 대명사다. 문제는 다음과 같다.
N * N 크기의 체스판에서 N개의 퀸을 서로 공격할 수 없도록 놓을 수 있는 경우의 수는? (N=4라고 가정)

먼저 위에서 언급했듯이, 백트래킹 알고리즘은 트리 구조를 기반으로 하기 때문에 상태공간을 트리 구조로 표현할 수 있어야한다.
위의 체스판(상태공간)을 트리 구조로 나타내면 다음과 같다.
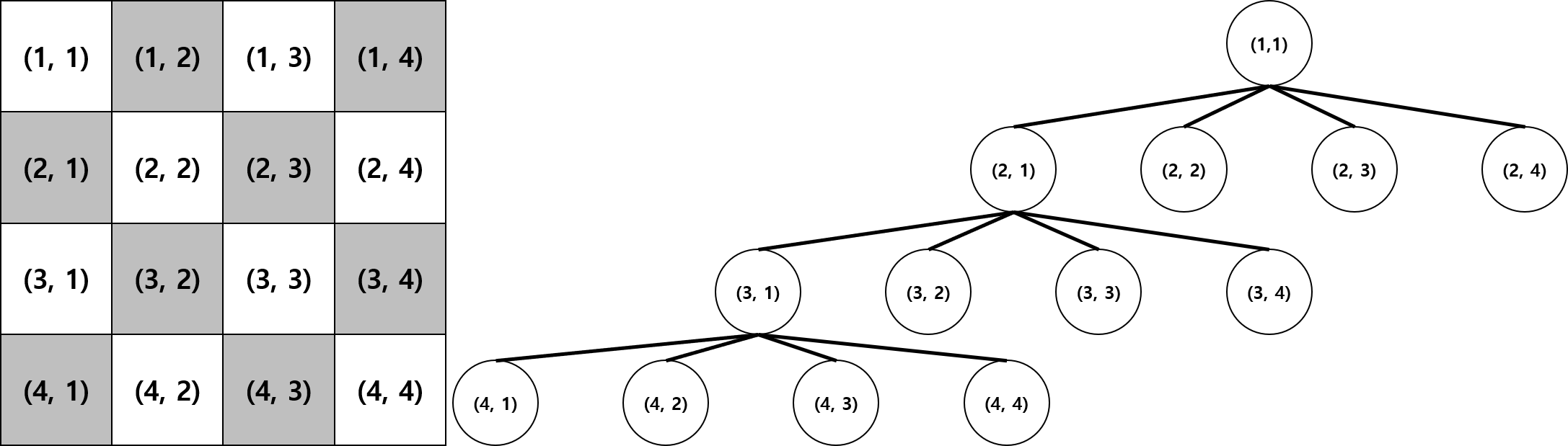
이제 (1, 1)을 시작 지점으로 보고 DFS를 진행하면 아래 그림의 모습이 나오게될 것이다.
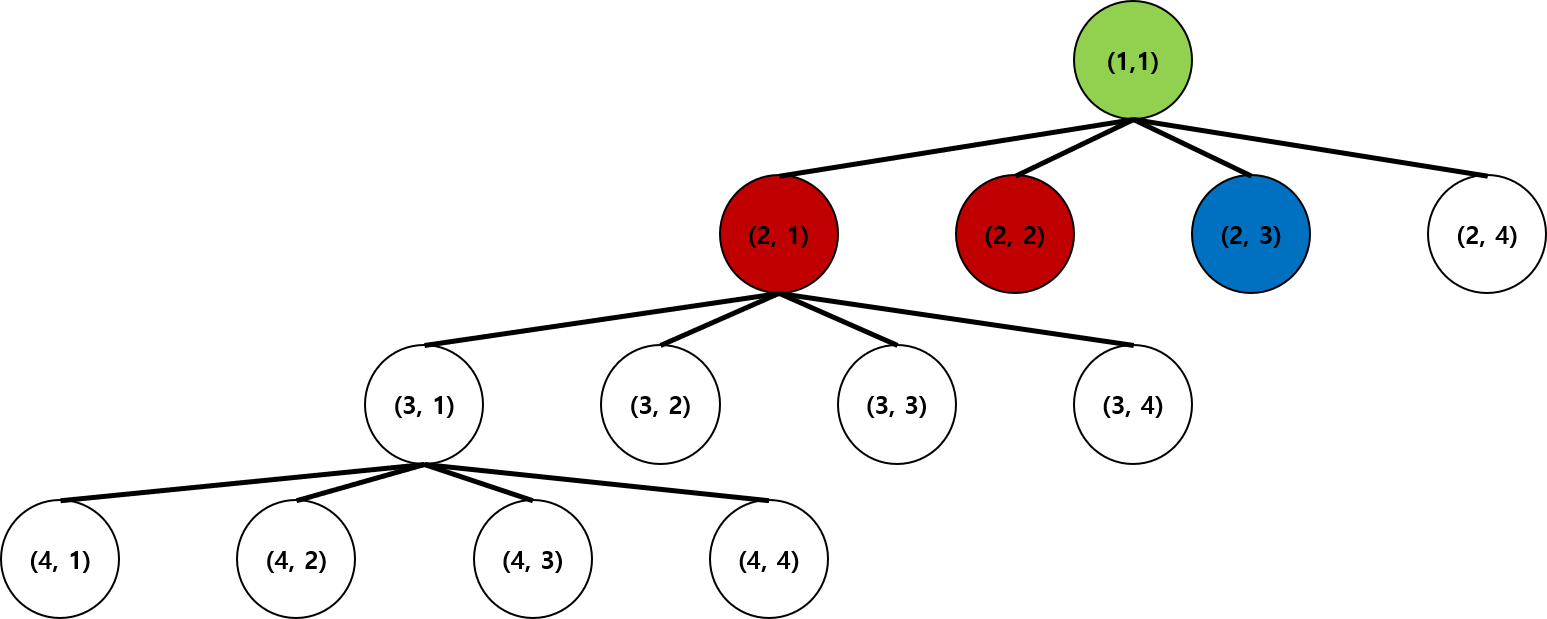
위의 그림을 설명하면 다음과 같다.
- (1, 1)을 시작 노드로 DFS 탐색을 진행한다.
- (2, 1)로 탐색을 내려가니 해당 지점은 (1, 1) 위치에 있는 퀸이 공격할 수 있는 위치이므로 조건에 맞지않는다. 따라서 가지치기(배제)를 한다. 즉, 해당 노드 아래 노드는 탐색을 진행하지 않는다.
- (2, 2)로 다음 탐색을 진행하니 마찬가지로 퀸이 공격할 수 있는 위치이므로 조건에 맞지 않는다. 가지치기(배제)를 한다.
- (2, 3)로 다음 탐색을 진행하니 해당 위치는 퀸이 공격할 수 없는 위치이므로 조건에 부합한다. 따라서 해당 노드를 기준으로 DFS(깊이 우선 탐색)를 진행한다.
만약 이 문제를 백트래킹이 아닌 단순 DFS로 푼다면, (4, 1)부터 비교를 하나하나해 나갈 것이다.
C++ 언어를 이용하여 코드로 살펴보자.
#include <iostream>
#include <cmath>
using namespace std;
int N;
int cnt = 0;
int* cols; // cols[level]은 level번째 깊이(행)에서 몇 번째 열에 퀸이 놓였는지를 담는다.
bool isPromising(int level) {
for (int i = 1; i < level; ++i) {
if (cols[i] == cols[level]) // 같은 열에 놓였는지를 검사한다.
return false;
else if ((level - i) == abs(cols[level] - cols[i])) // 같은 대각선에 놓였는지를 검사한다.
return false;
}
return true;
}
// 입력값은 다음과 같다.
// 1. 현재 어떤 레벨(깊이)인지
void queens(int level) {
if (!isPromising(level))
return;
else if (level == N) {
cnt += 1;
return;
}
for (int col = 1; col <= N; ++col) {
cols[level + 1] = col;
queens(level + 1);
}
}
int main() {
cin >> N;
cols = new int[N + 1];
for (int i = 0; i <= N; ++i)
cols[i] = 0;
queens(0);
cout << cnt << "\n";
delete[] cols;
return 0;
}
'Algorithm > Theory' 카테고리의 다른 글
| [자료구조] 그래프(Graph) (0) | 2019.12.10 |
|---|---|
| [자료구조] 서로소 집합(Disjoint-Set) (0) | 2019.11.13 |
| [알고리즘] 동적 계획법(Dynamic Programming) (0) | 2019.10.24 |
| [자료구조] 이분 그래프 (Bipartite Graph) (0) | 2019.09.24 |
| [자료구조] 쿼드 트리 (Quad Tree) (0) | 2019.08.29 |
댓글
이 글 공유하기
다른 글
-
[자료구조] 서로소 집합(Disjoint-Set)
[자료구조] 서로소 집합(Disjoint-Set)
2019.11.13 -
[알고리즘] 동적 계획법(Dynamic Programming)
[알고리즘] 동적 계획법(Dynamic Programming)
2019.10.24 -
[자료구조] 이분 그래프 (Bipartite Graph)
[자료구조] 이분 그래프 (Bipartite Graph)
2019.09.24 -
[자료구조] 쿼드 트리 (Quad Tree)
[자료구조] 쿼드 트리 (Quad Tree)
2019.08.29