[알고리즘] 세그먼트 트리 (SegmentTree)
1. 개요
구간 합 문제에서 세그먼트 트리가 사용됩니다. (꼭 합이 아니어도 구간의 최솟값이라든가 어떤 구간의 정보를 저장할 때 사용합니다. 🧐 )
다음의 두 가지 요구사항을 가지는 문제가 있습니다.
- (start, end) 구간에서 구간의 합을 구해야한다. (arr[start] + arr[start + 1] + ... + arr[end - 1] + arr[end])
- 특정 위치의 값이 빈번히 변경된다. (start + 10의 위치값을 v로 변경하기 등등)
요구사항 자체는 아주 간단하지만, 문제는 성능입니다.
단순 반복문을 이용하게 되면 위의 1번 연산은 $\mathcal{O}(N)$, 2번 연산은 $\mathcal{O}(1)$이 걸리게 됩니다.
위 연산이 최대 M번 수행된다고 할때 총 시간 복잡도는 $\mathcal{O}(NM)$ + $\mathcal{O}(M)$ = $\mathcal{O}(NM)$입니다. 😅
위에서 2번 연산(갱신)이 없다고 생각해보겠습니다.
변경되는 수가 없기 때문에 구간의 합을 미리 저장해놓는 방식으로 문제를 해결할 수 있습니다.
S[i] = A[1] + A[2] + ... + A[i - 1] + A[i] 일 때, i~j 구간의 합은 S[j] - S[i - 1] 로 나타낼 수 있습니다. (1~j 합에서 1~i 합을 뺀 것)
for (int i = 1; i < N; i++) {
S[i] = A[i] + S[i - 1];
}
이때 2번 연산으로 A[1]의 값이 변경되면 모든 S 배열이 갱신되어야 하기 때문에 $\mathcal{O}(N)$이 걸리게 됩니다.
즉, 위 요구사항을 만족할 수 있는 괜찮은 성능을 가지는 자료구조가 필요하다는 것이죠..
2. 세그먼트 트리 (SegmentTree) 란?
자료구조로 단순 배열 대신 세그먼트 트리를 이용하면 위의 1, 2번 연산 모두 $\mathcal{O}(\log N)$ 시간 복잡도로 처리가 가능합니다.
세그먼트 트리는 리프 노드와 리프 노드가 아닌 것으로 구분할 수 있으며, 각각의 의미는 다음과 같습니다.
- Leaf 노드: 각각의 수 (입력 값)
- Leaf 노드가 아닌 노드: 왼쪽 자식과 오른쪽 자식의 합 (구간의 합), 즉 구간에 대한 정보를 저장합니다.
N=10 일 때의 세그먼트 트리는 다음과 같습니다.

루트 노드를 보면 인덱스가 0이 아닌 1번부터 시작하는걸 볼 수 있는데, 이는 자식 노드의 인덱스를 쉽게 구하기 위함으로, 어떤 노드의 인덱스가 n일 때, 해당 노드의 왼쪽 자식의 노드는 2*n, 오른쪽 자식의 노드는 2*n+1 이 됩니다. (이진 트리 구현 기법)
int[] tree, arr; // 배열이 할당되어있다고 가정하자.
public int init(int start, int end, int nodeIdx) {
if (start == end) { // 리프 노드는 배열 원소의 값을 가진다.
return tree[nodeIdx] = arr[nodeIdx];
} else {
int mid = (start + end) / 2;
return tree[nodeIdx] = init(start, mid, nodeIdx * 2) + init(mid + 1, end, nodeIdx * 2 + 1);
}
}3. 세그먼트 트리에서 구간의 합 찾기
2~7 구간의 합을 찾고 싶다면 다음의 노드로 알 수 있다.
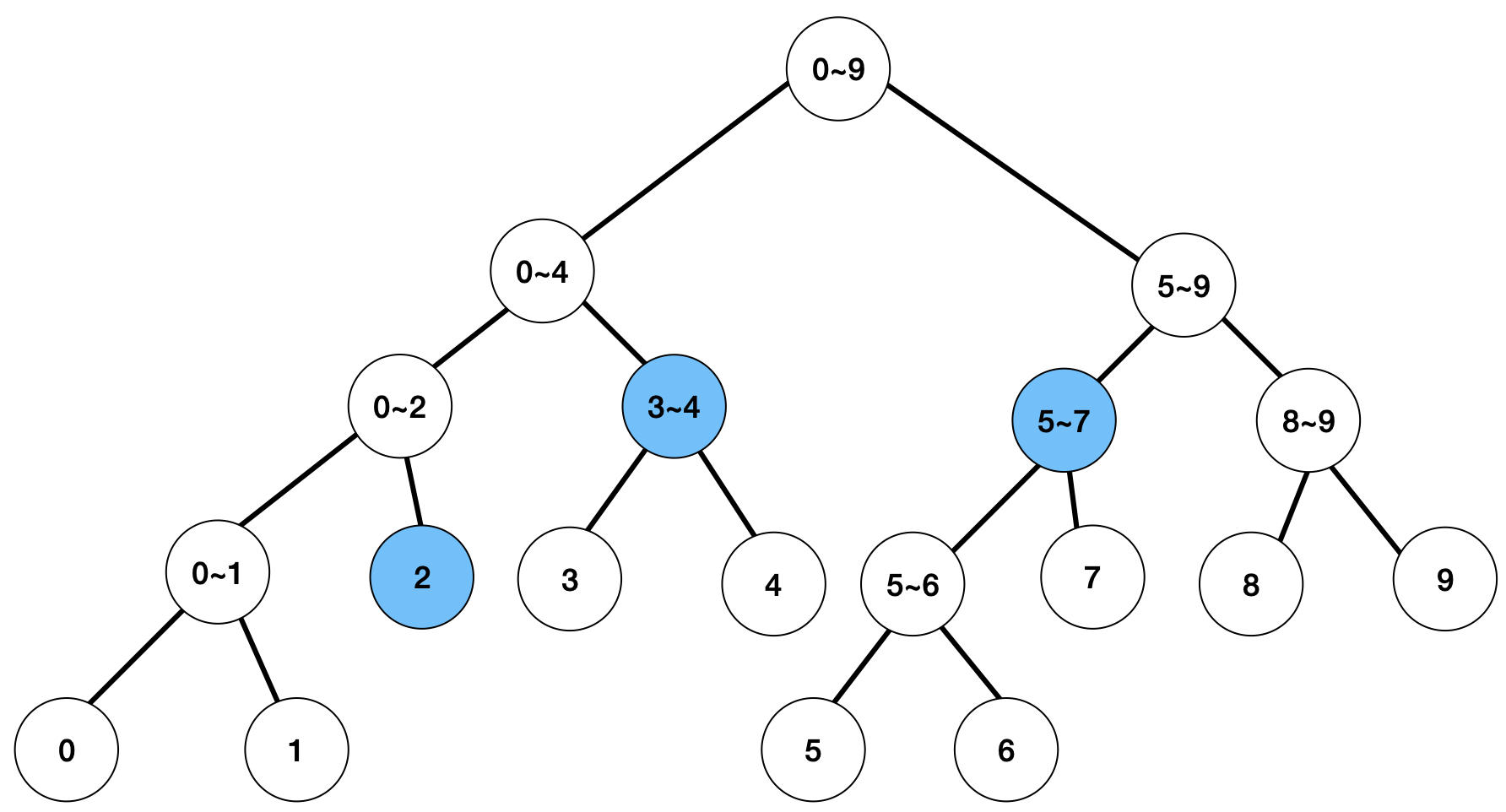
노드가 담당하고 있는 구간이 [start, end]이고, 합을 구해야하는 구간이 [left, right] 일때, 총 4가지 경우가 존재합니다.
- [left, right]와 [start, end]가 겹치지 않는 경우 ---> 더이상의 탐색이 무의미
- [left, right]가 [start, end] 구간을 완전히 포함하는 경우 ---> 해당 노드가 가진 구간의 합 데이터를 그대로 사용. (더이상 탐색 X)
left ㅣ--------------------ㅣ right
start ㅣ----------ㅣ end - [left, right]가 [start, end] 구간 안에 완전히 포함되는 경우 ---> 자식 노드로 탐색 진행
left ㅣ--------ㅣ right
start ㅣ----------------ㅣ end - [left, right]와 [start, end] 구간이 겹쳐져 있는 경우 ---> 자식 노드로 탐색 진행
left ㅣ-----------ㅣ right
start ㅣ----------ㅣ end
// 노드가 담당하고 있는 구간: [start, end]
// 합을 구해야하는 구간: [left, right]
public int sum(int start, int end, int nodeIdx, int left, int right) {
if (left > end || right < start) {
return 0;
}
if (left <= start && end <= right) {
return segmentTree[nodeIdx];
}
int mid = (start + end) / 2;
return sum(start, mid, nodeIdx * 2, left, right) + sum(mid + 1, end, nodeIdx * 2 + 1, left, right);
}
4. 특정 위치의 배열 원소 값 수정하기
특정 위치의 원소를 수정한다면, 그 수가 포함된 구간을 담당하는 노드를 모두 변경해줘야 합니다.
예를 들어, 7번째 수를 변경한다면, 변경이 필요한 노드는 다음과 같다.
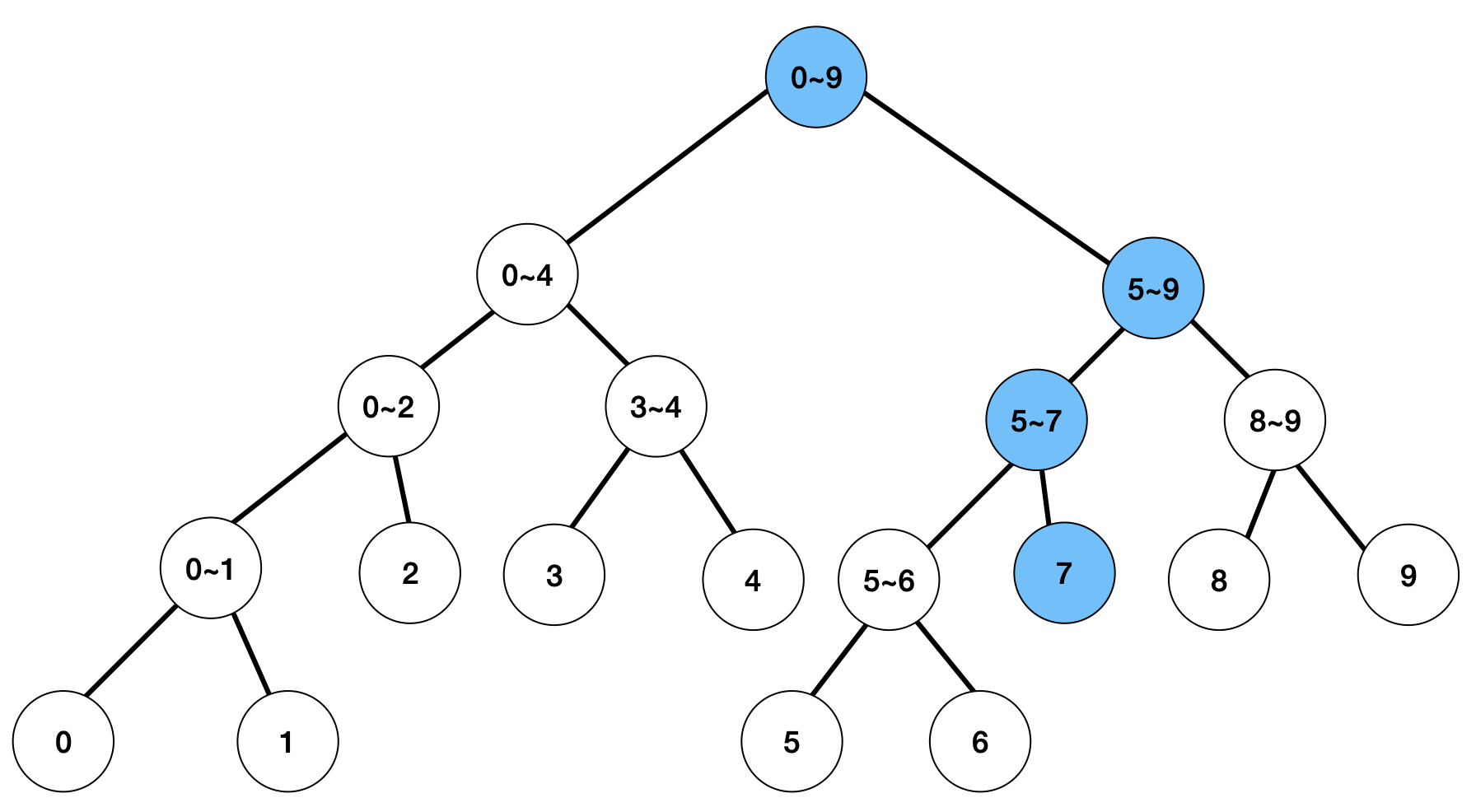
7번째 수를 150->155 로 수정한다고 했을 때, 기존값과 변경값의 차이는 5가 된다. 이 차이만큼 변경이 필요한 모든 노드들에 더해준다.
// updateIdx: 수정한 인덱스 값. (7번째 수를 변경했다면, 해당 파라미터 값은 7)
// diff: 기존값과 변경값의 차이값
public void update(int start, int end, int nodeIdx, int updateIdx, int diff) {
if (updateIdx < start || end < updateIdx) {
return;
}
segmentTree[nodeIdx] += diff;
if (start != end) {
int mid = (start + end) / 2;
update(start, mid, nodeIdx * 2, updateIdx, diff);
update(mid + 1, end, nodeIdx * 2 + 1, updateIdx, diff);
}
}
5. 세그먼트 트리의 사이즈 구하기
세그먼트 트리에서 원소 하나하나의 값을 담는 곳은 리프 노드다. 리프 노드를 제외한 노드는 모두 구간의 대표값을 저장한다. 따라서, 수열의 크기를 N이라면, 리프 노드가 N개인 이진 트리의 사이즈가 된다.
이진 트리의 특성에 따라 트리의 각 높이에 따른 노드의 수는 $2^{0}$, $2^{1}$, ..., $2^{height - 1}$ 이다. 예를 들어, 리프 노드의 수(=N)가 8개라면 트리의 높이는 4가 된다. (트리의 높이는 0부터 시작한다는걸 유의하자.)
이를 식으로 나타내면 $2^{k}$ >= N 을 만족하는 최소의 k를 찾아야한다. 양변에 log를 취하면 k >= log(N) / log(2) 이다. log(N)/log(2)의 값을 올림하게 되면 최소의 k값을 구할 수 있다. 트리의 높이는 0부터 시작하기 때문에 여기서 구한 k+1을 해주면 트리의 높이를 구할 수 있다. 따라서 전체 트리의 사이즈는 $2^{height}$ 가 된다.
class SegmentTree {
int[] tree;
public SegmentTree(int n) {
int k = (int) Math.ceil(Math.log(n) / Math.log(2));
int height = k + 1;
int size = (int) Math.pow(2, height);
tree = new int[size];
}
}
6. 게으른 전파(Lazy Propagation)
세그먼트 트리의 특성을 살려 하나의 원소에 대한 값의 수정(업데이트)이 아닌, a~b 구간에 대한 업데이트를 해야할 경우에 당장에 a~b 까지의 모든 리프 노드들에 대한 값의 수정이 일어날 필요는 없다는 것입니다.
만약, 1~5 구간의 원소들의 업데이트를 해야하는 경우라면 해당 구간을 나타내는 노드까지만 업데이트를 진행하는 것이죠.
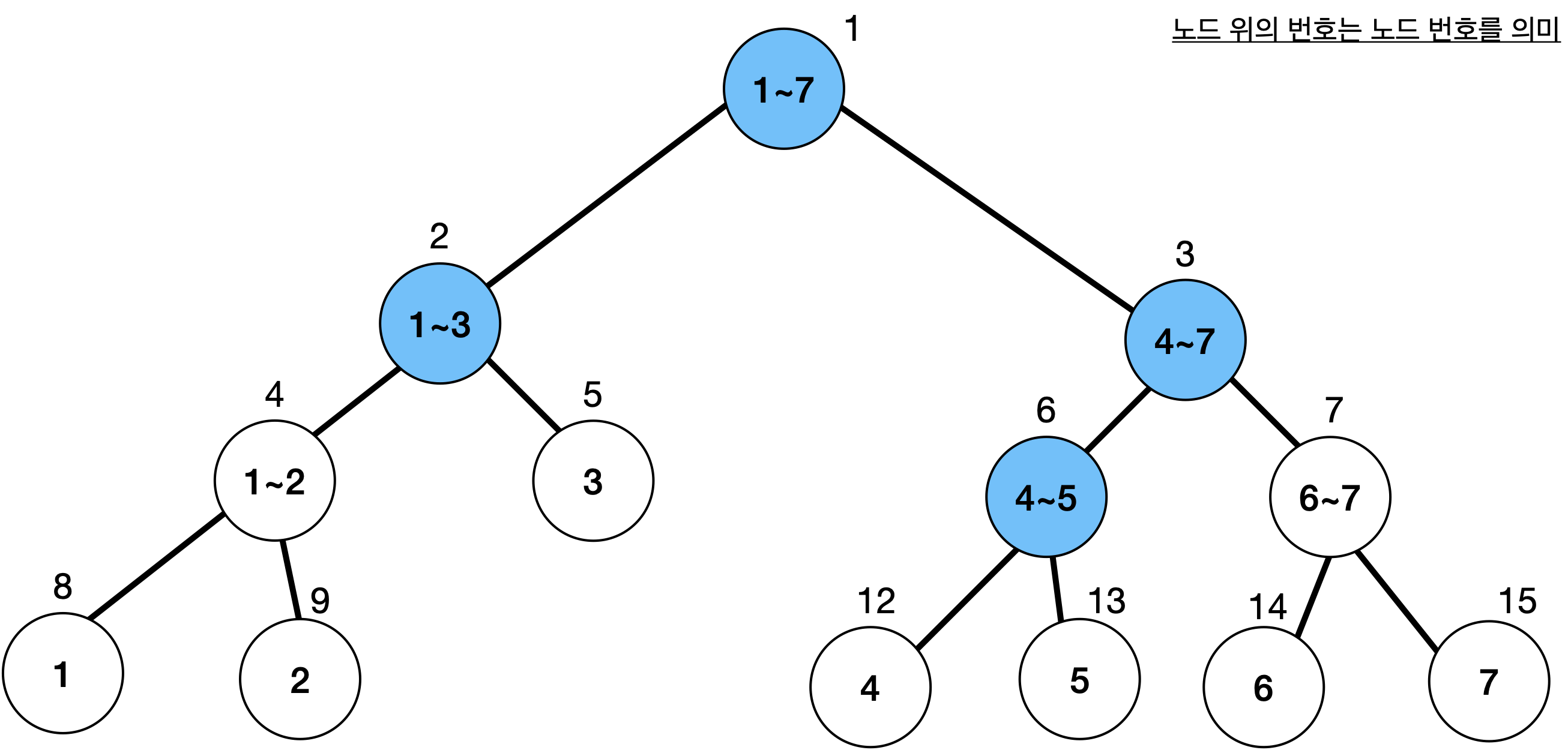
구간의 대표값을 저장하는 세그먼트 트리의 특성을 잘 생각해보면, 위 색칠된 노드들만 수정해줘도 당장의 요구사항은 만족한 셈입니다.
7. 참고자료
[1] www.acmicpc.net/blog/view/9
'Algorithm > Theory' 카테고리의 다른 글
| [알고리즘] 아호 코라식(Aho-Corasick) 알고리즘 (0) | 2021.03.16 |
|---|---|
| [알고리즘] KMP(Knuth-Morris-Pratt) 알고리즘 (0) | 2021.03.10 |
| [알고리즘] LIS(Longest Increasing Subsequence) (0) | 2021.03.03 |
| [알고리즘] 슬라이딩 윈도우(Sliding Window) 알고리즘 (0) | 2020.10.31 |
| [알고리즘] 투 포인터(Two Pointers) 알고리즘 (0) | 2020.10.26 |
댓글
이 글 공유하기
다른 글
-
[알고리즘] 아호 코라식(Aho-Corasick) 알고리즘
[알고리즘] 아호 코라식(Aho-Corasick) 알고리즘
2021.03.16 -
[알고리즘] KMP(Knuth-Morris-Pratt) 알고리즘
[알고리즘] KMP(Knuth-Morris-Pratt) 알고리즘
2021.03.10 -
[알고리즘] LIS(Longest Increasing Subsequence)
[알고리즘] LIS(Longest Increasing Subsequence)
2021.03.03 -
[알고리즘] 슬라이딩 윈도우(Sliding Window) 알고리즘
[알고리즘] 슬라이딩 윈도우(Sliding Window) 알고리즘
2020.10.31