[알고리즘] KMP(Knuth-Morris-Pratt) 알고리즘
1. 개요
문자열 매칭을 생각해보면,
ABABABAC // 원본 문자열 (S[i], 원본 문자열 길이 n)
ABAC // 찾을 문자열 (P[i], 찾을 문자열 길이 m)
위의 S 문자열에서 P 문자열을 찾는 패턴 매칭에서 가장 단순(Naive)한 방법은 다음과 같습니다.
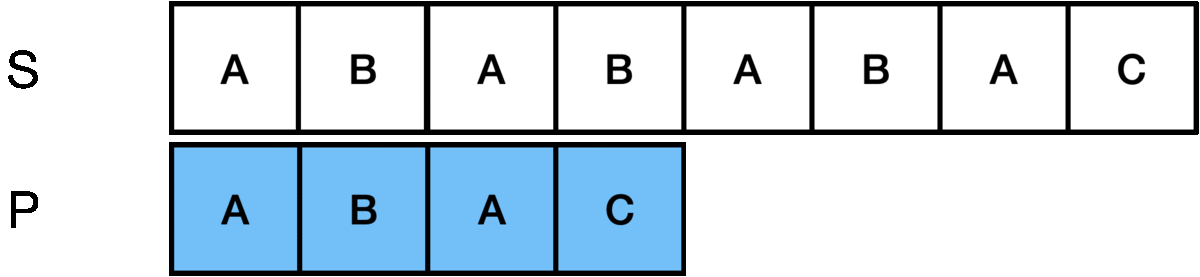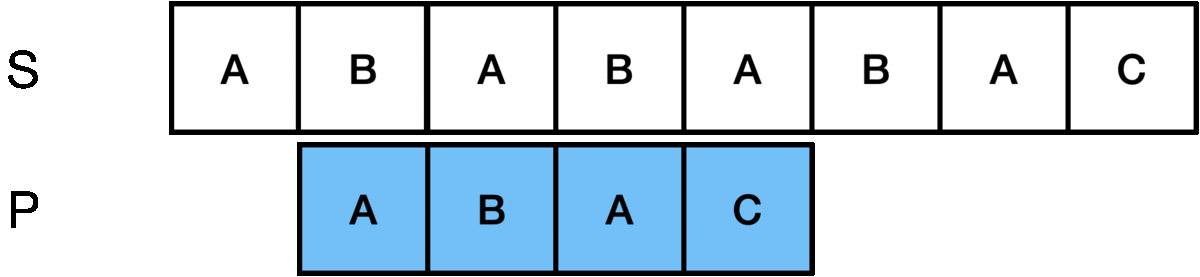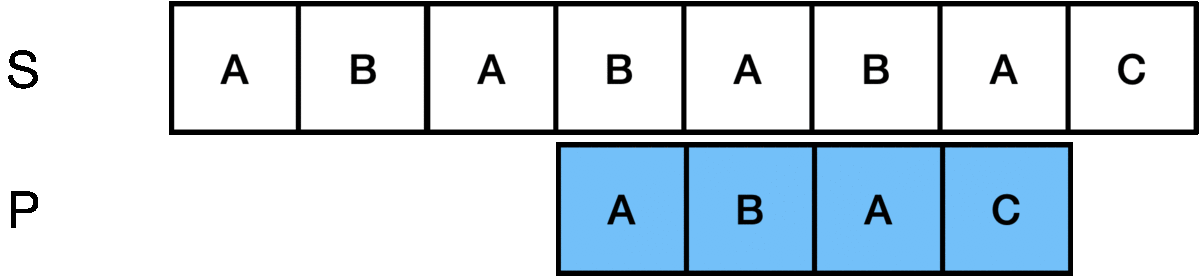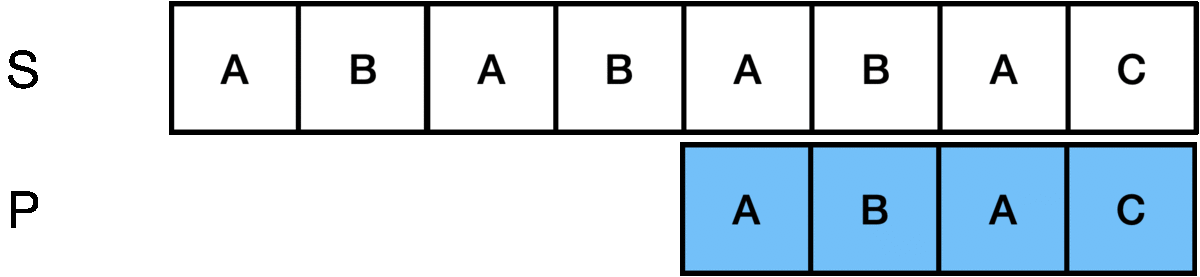
첫 번째 인덱스부터 P 문자열의 길이인 m만큼 비교해보고 불일치하면 다음 인덱스로 이동한 후 다시 첫 문자부터 비교합니다.
이 똑같은 행동을 n-m-1 인덱스까지 반복하기에 총 시간 복잡도는 O(nm) 이 걸리게 됩니다.
2. KMP (Knuth-Morris-Pratt) 알고리즘이란?
문자열 매칭(또는 패턴 매칭) 알고리즘은 대표적으로 3가지가 있습니다.
- KMP 알고리즘
- Rabin-Karp 알고리즘
- Boyer-Moore 알고리즘
KMP 알고리즘은 패턴 매칭에 사용되는 알고리즘 중 하나로 시간 복잡도는 O(n+m) 입니다.
아이디어는 간단합니다. 첫 번째 인덱스에서의 비교를 보겠습니다.
A B A B A B A C
A B A C <--- 끝 문자 C는 불일치했지만 그 전까지의 문자(ABA)는 일치합니다. 이를 활용할 순 없을까요? 🤔
우리가 얻은 일치하는 문자열에 대해 Prefix(접두사)와 Suffix(접미사)의 일치여부를 확인합니다.
몇 가지 예시로 살펴보자겠습니다.
(Prefix는 파랑색, Suffix는 주황색으로 표시, lcs 배열은 해당 문자열에서 Prefix-Suffix가 일치하는 문자의 갯수)
예시 1)
ABA <-- 일치 ABA <-- 불일치 Prefix는 AB
ABA ABA Suffix는 BA
longestCommonSuffix[2] = 1
예시 2)
ABCCAB <-- 불일치 ABCCAB <-- 일치 ABCCAB <-- 불일치 Prefix는 ABC
ABCCAB ABCCAB ABCCAB Suffix는 CAB
longestCommonSuffix[5] = 2
예시 3)
ABABAB <-- 불일치 ABABAB <-- 일치 ABABAB <-- 일치
ABABAB ABABAB ABABAB
longestCommonSuffix[5] = 4
원본 문자열이 A B C C A B D D D D D D D D
찾는 문자열이 A B C C A B E
위의 조건에서 일치하는 문자열에 대해 Prefix-Suffix를 확인하면 다음과 같은 인덱스 이동이 가능해집니다.

위 과정은 다음과 같습니다.
- 0번 인덱스에서 origin 문자열과 pattern 문자열을 비교했더니, 마지막 E에서 불일치가 발생했고, 그 전까지의 문자열은 일치한다는 정보를 얻었습니다.
- 그 전까지의 문자열 A B C C A B 에 대한 Prefix-Suffix 일치 갯수는 위에서 살펴본 예시 2번과 같이 2개입니다.
Naive한 방법이라면 다음 비교를 위해 1번 인덱스로 이동해서 다시 문자열을 비교했겠지만,
KMP에서는 0번 다음으로 4번 인덱스로 바로 이동합니다..!
위와 같이 가장 긴 Prefix-Suffix가 같은 갯수(Longest Common Suffix, 이하 LCS)를 구하는 코드는 다음과 같습니다. 🧐
int[] getLcs(String pattern) {
int len = pattern.length();
int[] lcs = new int[len];
int j = 0;
for (int i = 0; i < len; i++) {
while (j > 0 && pattern.charAt(i) != pattern.charAt(j)) {
j = lcs[j - 1];
}
if (pattern.charAt(i) == pattern.charAt(j)) {
lcs[i] = ++j;
}
}
return lcs;
}위에서 구한 LCS 배열을 가지고 KMP 알고리즘을 이용해 패턴 매칭을 하는 코드는 다음과 같습니다.
int kmp(String origin, String pattern) {
// 1. longestCommonSuffix 배열을 얻어옵니다.
int[] lcs = getLcs(pattern);
int j = 0;
for (int i = 0; i < origin.length(); i++) {
// 원본 문자열: A B C C A B D ...
// 찾는 문자열: A B C C A B E
// i=6, j=6 일때 문자 불일치가 발생하기 때문에 그 전 문자열의 접두사-접미사 갯수를 확인해야한다.
// pi[5]=2로 AB가 일치한다. 배열의 인덱스는 0번부터 시작하기 때문에 이 값을 그대로 j에 대입하면,
// AB 다음 문자인 C부터 다시 비교에 들어가게 된다.
while (j > 0) && origin.charAt(i) != pattern.charAt(j)) {
j = lcs[j - 1];
}
// 문자가 일치했다면 j 인덱스 증가.
// 만약 j 인덱스가 찾는 문자열의 길이-1과 같다면, 즉 완전히 일치했다면,
// 다음 i번부터는 처음부터 비교를 해야하기 때문에 j를 0으로 초기화한다.
if (origin.charAt(i) == pattern.charAt(j)) {
if (j == pattern.length() - 1) {
j = lcs[j];
} else {
j++;
}
}
}
}3. 참고자료
'Algorithm > Theory' 카테고리의 다른 글
| [자료구조] Trie(트라이) (0) | 2021.09.03 |
|---|---|
| [알고리즘] 아호 코라식(Aho-Corasick) 알고리즘 (0) | 2021.03.16 |
| [알고리즘] 세그먼트 트리 (SegmentTree) (0) | 2021.03.05 |
| [알고리즘] LIS(Longest Increasing Subsequence) (0) | 2021.03.03 |
| [알고리즘] 슬라이딩 윈도우(Sliding Window) 알고리즘 (0) | 2020.10.31 |
댓글
이 글 공유하기
다른 글
-
[자료구조] Trie(트라이)
[자료구조] Trie(트라이)
2021.09.03 -
[알고리즘] 아호 코라식(Aho-Corasick) 알고리즘
[알고리즘] 아호 코라식(Aho-Corasick) 알고리즘
2021.03.16 -
[알고리즘] 세그먼트 트리 (SegmentTree)
[알고리즘] 세그먼트 트리 (SegmentTree)
2021.03.05 -
[알고리즘] LIS(Longest Increasing Subsequence)
[알고리즘] LIS(Longest Increasing Subsequence)
2021.03.03